perawat.org | cara menentukan populasi, teknik sampling, dan rumus sampel penelitian keperawatan.
Kegiatan penelitian di bidang keperawatan atau kesehatan dapat dilakukan dengan benar apabila peneliti paham betul tentang populasi dan sampel yang akan diteliti (Indarwati, 2020).
Menentukan populasi dan sampel sangat penting agar penelitian menjadi efektif dan efisien.
Anda harus mampu mengevaluasi diri sendiri dalam menentukan populasi dan sampel.
Jangan memilih populasi dan sampel yang tidak akan dapat anda selesaikan.
Contohnya, anda ingin melakukan penelitian untuk mengidentifikasi faktor-faktor yang berhubungan dengan pengetahuan perawat tentang resusitasi jantung paru di Indonesia.
Populasinya adalah seluruh Perawat di Indonesia.
Apakah salah?
Tentu saja tidak, tetapi apakah anda dapat mencapainya dalam kurun waktu penelitian yang ditentukan?
Apakah boleh?
Tentu boleh, namun sekali lagi, apakah anda dapat mengumpulkan data dalam waktu yang ditentukan?
Seluruh penelitian, baik itu penelitian tugas kuliah seperti skripsi atau tesis, ataupun penelitian yang mendapatkan pendanaan dari pihak luar, memiliki jangka waktu.
Katakanlah skripsi atau tesis yang harus selesai dalam 6 bulan.
Tetapi karena populasi anda yang sangat luas, waktu pengumpulan data anda menjadi lebih lama.
Ujung-ujungnya, yang lain sudah sidang atau sudah selesai penelitian, anda baru akan melakukan analisa data, belum lagi revisi konsul pembimbing dan lain sebagainya.
BACA JUGA: 10 Prioritas Penelitian Keperawatan di Indonesia
Oleh karena itu, sangat penting menentukan populasi dan sampel.
Dalam artikel ini, kita akan belajar cara menentukan Populasi, Teknik Sampling, dan Rumus Sampel.
Namun sebelumnya, mari kita lihat dahulu konsep-konsep dasar dari populasi, sampel, dan teknik sampling berikut…
atau langsung lompat di bagian yang anda inginkan melalui daftar isi:
Daftar isi
Populasi
Sebelum mempelajari Teknik Sampling, dan Rumus Sampel, mari kita lihat cara menentukan Populasi terlebih dahulu.
Populasi adalah wilayah generalisasi yang terdiri atas subjek atau objek yang ditentukan oleh peneliti untuk diteliti dan selanjutkan akan ditarik kesimpulannya (Indarwati, 2020).
Menurut Adiputra (2021), populasi bukan hanya orang, tetapi juga objek dan benda-benda alam yang lain.
Orang, benda, lembaga, organisasi, dan sebagainya yang menjadi sasaran penelitian merupakan anggota populasi.
Anggota populasi yang terdiri dari orang-orang biasa disebut dengan subjek penelitian, sedangkan anggota penelitian yang terdiri dari benda-benda atau yang bukan orang disebut dengan objek penelitian (Adiputra, 2021).
Jenis-Jenis Populasi
Berdasarkan jumlahnya, populasi dapat dibedakan menjadi:
- Populasi Terbatas atau populasi terhingga (definite)
- Populasi Tak Terbatas atau populasi tak terhingga (indefinite)
Berdasarkan keterjangkauannya, populasi dibedakan menjadi:
- Populasi Target (populasi tidak terjangkau)
- Populasi Sumber (populasi terjangkau)
Sedangkan berdasarkan jenisnya, populasi dibedakan menjadi:
- Populasi Homogen
- Populasi Heterogen
Waduh banyak juga ya…
Mari kita lihat satu-satu biar lebih jelas.
Populasi Terbatas
Populasi terbatas atau populasi terhingga (definite) adalah populasi yang dapat dihitung.
Populasi ini memiliki batas kuantitatif yang jelas karena memiliki karakteristik yang terbatas.
Contohnya adalah luas daerah, jumlah pasien, jumlah murid, jumlah balita, dsb.
Populasi Tak Terbatas
Populasi tak terbatas atau populasi tak terhingga (indefinite) adalah populasi yang mempunyai jumlah yang tak terbatas.
Berbeda dengan populasi terbatas yang memiliki batas kuantitatif yang jelas, populasi tak terbatas tidak dapat ditemukan batas-batasnya.
Karena batasnya tidak dapat ditemukan, maka tidak dapat dinyatakan dalam bentuk jumlah secara kuantitatif.
Contohnya adalah pasir di pantai, padi di sawah, dan lainnya.
Populasi Target
Populasi Target atau populasi tidak terjangkau adalah populasi yang akan menjadi sasaran akhir penerapan hasil penelitian (Adiputra, 2021).
Populasi target bersifat umum dan luas.
Misalnya, penelitian mengenai “kepatuhan minum obat anti tuberkulosis (OAT) oleh penderita TB Paru di DKI Jakarta.”
Dalam penelitian ini populasinya adalah seluruh pasien TB Paru yang ada di Wilayah Provinsi DKI Jakarta.
Berarti seluruh pasien TB Paru di DKI Jakarta merupakan populasi target.
Populasi Sumber
Populasi sumber atau populasi terjangkau adalah bagian dari populasi target yang dapat dijangkau oleh peneliti (Adiputra, 2021).
Secara sederhana, populasi sumber merupakan bagian dari populasi target yang dibatasi oleh tempat dan waktu yang lebih sempit.
Lihat contoh populasi target sebelumnya.
Populasi target adalah seluruh pasien TB Paru di DKI Jakarta.
Mari kita buat populasi tersebut lebih sempit.
Alih-alih DKI Jakarta, kita hanya akan melakukan penelitian di satu kota di Provinsi DKI Jakarta, yaitu Jakarta Utara.
Sehingga penelitian kita menjadi, “kepatuhan minum obat anti tuberkulosis (OAT) oleh penderita TB Paru di Jakarta Utara.”
Berarti, seluruh pasien TB Paru di Jakarta Utara merupakan populasi sumber.
Populasi Homogen
Populasi homogen adalah populasi yang unsur-unsurnya memiliki sifat yang sama (Adiputra, 2021).
Misalnya, seorang dokter yang akan melihat golongan darah seseorang, maka ia cukup mengambil setetes darah saja.
Dokter tersebut tidak perlu mengambil satu botol, sebab setetes dan sebotol darah hasilnya tetap sama.
Populasi Heterogen
Populasi heterogen adalah populasi yang unsur-unsurnya memiliki sifat atau keadaan yang bervariasi, sehingga perlu ditetapkan batas-batasnya, baik secara kualitatif maupun secara kuantitatif (Adiputra, 2021).
Misalnya, jumlah remaja di Semarang, dan jumlah penderita ISPA di Jakarta.
Sampel
Setelah mempelajari cara menentukan Populasi, selanjutnya adalah mempelajari Sampel atau Teknik Sampling, baru kemudian akan kita lanjurkan dengan Rumus Sampel.
Sampel adalah bagian dari populasi, atau miniatur dari populasi yang akan diteliti.
Sampel yang baik adalah yang dapat mewakili karakteristik (representatif) yang ada pada populasi (Indarwati, 2020).
Mengapa kita perlu menentukan sampel penelitian?
Lagi-lagi adalah demi efisiensi proses penelitian yang akan kita lakukan.
Contoh kita akan melakukan penelitian tentang sikap perawat terhadap penggunaan telenursing dalam pelayanan keperawatan di DKI Jakarta.
Bila kita tidak mengambil sampel, maka kita harus mengukur sikap 50rb lebih perawat di DKI Jakarta.
Berapa lama waktu yang dibutuhkan untuk pengumpulan data?
Belum lagi berapa biaya yang dibutuhkan untuk itu.
Karena keterbatasan waktu, tenaga, dan dana penelitian, maka kita perlu menentukan sampel penelitian.
Dalam menentukan sampel, kita harus benar-benar memastikan bahwa sampel yang kita pilih harus memiliki karakteristik yang sama dengan populasi.
Adiputra (2021) menyebutkan ada beberapa ciri-ciri sampel yang baik, yaitu:
- Sampel dipilih dengan cara hati-hati, dengan menggunakan cara tertentu dengan benar;
- Sampel harus mewakili populasi (representatif), sehingga gambaran yang diberikan mewakili keseluruhan karakteristik yang terdapat pada populasi;
- Besarnya ukuran sampel hendaklah mempertimbangkan tingkat kesalahan sampel yang dapat ditoleransi dan tingkat kepercayaan yang dapat diterima secara statistik;
- Sederhana dan mudah dilaksanakan;
- Memberikan keterangan sebanyak mungkin dengan biaya yang efisien.
Agar sampel yang kita tentukan dapat dipercaya, maka cara penarikan sampelnya harus dilakukan dengan seksama.
Cara pemilihan sampel ini disebut dengan teknik pengambilan sampel atau teknik sampling.
Teknik Sampling
Indarwati (2020) menyebutkan bahwa teknik sampling adalah cara menentukan sampling yang baik agar hasil penelitian dapat di generalisasikan kepada populasi yang diteliti.
Untuk menentukan sampel yang akan digunakan dalam penelitian, terdapat berbagai teknik sampling yang dapat digunakan (lihat gambar dibawah).

Probability sampling adalah teknik sampling yang memberikan peluang yang sama bagi setiap unsur (anggota) populasi untuk dipilih menjadi anggota sampel.
Sedangkan non probability sampling adalah teknik yang tidak memberi peluang/kesempatan yang sama bagi setiap unsur atau anggota populasi untuk dipilih menjadi sampel.
Hal ini dikarenakan pengambilan sampel tidak didasarkan atas kemungkinan yang dapat diperhitungkan, melainkan semata-mata hanya berdasarkan aspek-aspek kepraktisan saja.
Mari kita lihat satu persatu ketujuh teknik sampling turunan dari probability dan non-probability sampling diatas…
Simple Random Sampling
Simple random sampling atau pengambilan sampel acak sederhana adalah pengambilan sampel yang dilakukan sedemikian rupa sehingga setiap unit sampling mempunyai kesempatan yang sama untuk diambil sebagai sampel (Indarwati, 2020).
Cara sederhana untuk menggunakan teknik sampling ini adalah:
- Buat daftar semua unit sampel, disusun dan diberi nomor secara berurutan
- Buat gulungan kertas dan diberi nomor 0 sampai 9 (seperti arisan), atau sesuaikan dengan besarnya populasi (misalnya 0 sampai 3 pada populasi berjumlah 300 orang).
- Kocok dan ambil sesuai jumlah digit
Contoh simple random sampling:
Populasi penelitian kita berjumlah 500 orang.
Ke-500 orang tersebut dibuat daftar, disusun, dan beri nomor secara berurutan dari 1 sampai 500.
Buat 6 gulungan kertas arisan. Tulis angka 0, 1, 2, 3, 4, 5.
Kocok, dan lihat angka yang keluar (misalnya 1), lalu kembalikan kedalam botol lagi.
Kocok lagi hingga 3 kali (misal keluar 158), maka salah satu sampel yang kita masukan sebagai responden penelitian adalah sampel nomor 158 dari 500 orang pada daftar yang telah kita buat.
Jika angka pertama yang keluar adalah 5, tetap lanjutkan sebanyak 3 kali.
Misalnya angka yang keluar adalah 598, maka ambil sampel nomor 98, karena populasi kita hanya 500 saja.
Stratified Random Sampling
Stratified random sampling atau sampel acak distrata adalah pengambilan sampel yang dilakukan dengan membagi populasi menjadi beberapa strata, dimana setiap strata adalah homogen, sedangkan antar strata terdapat sifat yang berbeda kemudian dilakukan pengambilan sampel pada setiap strata (Indarwati, 2020).
Cara pengambilan sampel demikian disebut pengambilan sampel acak dengan stratifikasi.
Contoh stratified random sampling:
Seorang kepala ruangan ingin mengetahui prestasi kerja 12 orang perawat yang diukur berdasarkan kepatuhan dalam menggunakan SOP dalam memberikan pelayanan kepada pasien.
12 orang Perawat (populasi) kemudian dibagi menjadi 4 kelompok berdasarkan prestasi kerja tahun yang lalu.
Masing-masing kelompok terdiri dari 3 orang Perawat dengan prestasi kerja yang hampir sama dan terdapat perbedaan antar kelompok.
Kemudian pada setiap kelompok akan diambil 1 orang sebagai sampel hingga diperoleh total sampel sebanyak 4 orang.
Dengan cara demikian akan diperoleh 84 kombinasi.
Bila kita menggunakan simple random sampling maka akan diperoleh sebanyak 495 kombinasi.
Ini berarti bahwa dengan menggunakan stratified random sampling, kombinasi akan berkurang 411 atau 84% kombinasi yang tidak memperoleh peluang untuk terambil menjadi sampel.
Namun dengan pengambilan stratified random sampling setiap unit mempunyai peluang sama maka hasilnya tidak akan menimbulkan bias.
Tingkat ketepatan bila menggunakan stratified random sampling lebih tinggi bila dibandingkan simple random sampling (Indarwati, 2020).
Multistage Random Sampling
Multistage random sampling atau pengambilan sampel acak bertahap adalah pengambilan sampel acak yang tehnik pelaksanaannya dilakukan dengan membagi populasi menjadi beberapa fraksi kemudian diambil sampelnya (Indarwati, 2020).
Hasil pengambilan dari fraksi tersebut dibagi lagi menjadi fraksi-fraksi yang lebih kecil, kemudian diambil sampelnya lagi.
Pembagian ini dilakukan terus hingga mencapai unit sampel yang diinginkan.
Unit sampel yang terambil pertama disebut sebagai Primary Sampling Unit (PSU).
Multistage random sampling cocok untuk dipilih apabila kita ingin mengambil sampel yang tidak banyak pada populasi yang besar.
Contoh multistage random sampling dengan PSU kecil:
Kita akan melakukan berkaitan tentang pola pemanfaatan sarana pelayanan oleh pasien disebuah rumah sakit.
Rumah sakit disini merupakan populasi studi dengan ruangan sebagai unit sampel dan departemen sebagai PSU.
Dari sejumlah PSU tersebut diambil sampel dengan cara acak sederhana kemudian sampel departemen dibagi menjadi divisi dan diambil sampelnya.
Selanjutnya dari sampel divisi tersebut diambil lagi sampel ruangan dan semua pasien di ruangan tersebut merupakan sasaran penelitian.
Contoh multistage random sampling dengan PSU besar:
Kita akan melakukan berkaitan tentang perilaku hidup bersih sehat masyarakat disebuah kota
Kota dibagai menjadi wilayah (misalnya ada 4 wilayah), maka wilayah menjadi PSU.
Ambil satu wilayah secara acak untuk menjadi sampel.
1 wilayah tersebut kemudian dibagi kembali menjadi kecamatan, dan pilih satu kecamatan untuk menjadi sampel.
Kecamatan dibagi lagi menjadi kelurahan, dan pilih satu untuk menjadi sampel.
Demikian sampai seterusnya hingga ke tingkat RT.
Bila sudah sampai ke tingkat RT, akhirnya seluruh masyarakat (sesuai kriteria inklusi dan eksklusi) dalam RT tersebut diambil sebagai sampel penelitian.
Systematic Random Sampling
Systematic random sampling atau pengambilan sampel acak sistematik adalah pengambilan sampel secara acak yang dilakukan secara berurutan dengan interval tertentu (Indarwati, 2020).
Besar interval (i) dapat ditentukan dengan membagi populasi (N) dengan jumlah sampel yang diinginkan (n).
Rumusnya adalah:
i=N/n.
Contoh systematic random sampling:
Kita akan melakukan penelitian untuk mengetahui karakteristik penderita TB paru di sebuah kecamatan.
Populasi diketahui berjumlah 100 orang.
Pertama, kita harus menentukan ukuran sampel ideal terlebih dahulu.
Berapa ukuran sampel ideal untuk sebuah populasi? Kita akan membahasnya lebih lanjut pada bagian akhir artikel ini.
Misalnya, sampel ideal yang kita inginkan adalah 25 orang.
Setelah mengetahui ukuran sampel ideal selanjutnya kita akan menentukan interval sampel.
Interval sampel ini akan menjadi jarak standar antar nomor pada populasi.
Gunakan rumus diatas untuk menentukan interval.
i = N/n
i = 100/25
i = 4
Interval kita adalah 4.
Maka sampel yang kita pilih adalah 25 orang dari 100 orang yang memiliki nomor dengan interval 4 sesuai urutan.
Misalnya 1, 4, 8, 12, 16, dan seterusnya.
Accidental Sampling
Accidental sampling atau sampling seadanya adalah teknik pengambilan sampel dari sebagian populasi berdasarkan kemudahannya mendapatkan data tanpa perhitungan apapun atau seadanya saja (Indarwati, 2020).
Cara pengambilan sampel ini sudah banyak ditinggalkan pada penelitian dibidang Kesehatan, namun masih sering digunakan peneliti di bdiang sosial, ekonomi, dan politik untuk mengetahui opini masyarakat tentang suatu isu tertentu.
Contoh accidental sampling:
Kita akan melakukan penelitian mengenai pendapat masyarakat tentang profesi Perawat di DKI Jakarta.
Untuk mendapatkan sampel, kita hanya berdiri di pinggir jalan saja sambil bertanya pada masyarakat yang sedang lewat apakah mereka tahu tentang Perawat, dan lain sebagainya.
Quota Sampling
Quota sampling atau sampling berjatah hampir sama dengan teknik accidental sampling.
Perbedaannya hanya dalam quota sampling ada kontrol yang harus dilakukan, sehingga dapat mengurangi adanya bias.
Teknik quota sampling ini pengambilannya sangat bergantung pada peneliti, tetapi dengan kriteria dan jumlah yang telah ditentukan sebelumnya.
Contoh quota sampling
Kita akan melakukan penelitian tentang tingkat pengetahuan ibu tentang imunisasi dasar lengkap.
Dengan menggunakan quota sampling, kita harus menentukan jumlah sampel minimal yang harus diambil terlebih dahulu, misal 100 ibu yang mempunya anak umur kurang dari 1 tahun.
100 ibu tersebut kita bagi berdasarkan kuota, yaitu 50 ibu di wilayah kota, dan 50 ibu di wilayah desa.
Purposive Sampling
Purposive sampling adalah pengambilan sampel melalui pertimbangan-pertimbangan atau tujuan.
Cara pengambilan sampel ini dilakukan apabila peneliti mempunyai pertimbangan-pertimbangan tertentu.
Teknik sampling ini akan baik hasilnya apabila dilakukan oleh peneliti yang ahli dan memahami populasi tersebut (Indarwati, 2020).
Teknik sampling ini juga sangat cocok untuk penelitian studi kasus.
Contoh purposive sampling:
Kita akan melakukan penelitian tentang pengelolaan pasien gagal ginjal kronik yang menjalani terapi hemodialisa.
Tujuan penelitian yang kita lakukan adalah untuk mendeskripsikan bagaimana kepuasan pasien atas asuhan keperawatan yang dilakukan oleh Perawat saat menjalani hemodialisa.
Kita sebagai peneliti tentunya akan memilih sampel dengan pertimbangan-pertimbangan khusus, contohnya pasien gagal ginjal kronik yang sudah menjalani hemodialisa sebanyak > 10 kali, dan lain sebagainya.
Menghitung Jumlah Sampel Ideal
Setelah mempelajari cara menentukan Populasi dan Teknik Sampling, selanjutnya adalah Rumus Sampel.
Penentuan besar sampel dalam suatu penelitian tergantung pada apakah jumlah populasinya telah diketahui sebelumnya atau tidak.
Penentuan besar sampel juga tergantung dari hal-hal berikut ini (Adiputra, 2021):
- Biaya yang tersedia, waktu dan tenaga yang akan melaksanakan
- Variasi yang ada dalam variabel yang akan diteliti serta banyaknya variabel yang akan diteliti. Semakin heterogen populasi maka semakin besar sampel yang dibutuhkan.
- Presisi, atau ketepatan yang dikehendaki, semakin besar sampel kemungkinan akan lebih tepat menggambarkan populasi. Tetapi semakin besar sampel kemungkinan membuat kesalahan pada saat pengukuran juga akan menjadi besar (error meningkat)
- Rencana analisis, kalau analisis hanya manual tidak mungkin menganalisis data yang banyak sekali, berbeda dengan analisis menggunakan perangkat lunak computer
Rumus sampel bila jumlah populasi diketahui
Berikut adalah rumus sampel bila jumlah populasinya sudah kita ketahui (Adiputra, 2021):

Keterangan:
n : besar sampel
N : besar populasi
Z(1-a/2) : nilai sebaran normal baku, besarnya tergantung tingkat kepercayaan (TK), jika TK 90%, maka nilai 1,64, TK 95% = 1,96, TK 99% = 2,57.
P : Proporsi kejadian (jika proporsi kejadian tidak diketahui, maka dianjurkan = 0,5)
d : besar penyimpangan terhadap populasi yang diinginkan. Jika 10% maka d = 0,1, 5% = 0,05., 1% = 0,01.
Contoh penghitungan jumlah sampel dengan rumus sampel populasi diketahui:
Kita akan melakukan penelitian untuk mengidentifikasi hubungan aktivitas fisik dengan kejadian DM di sebuah Puskesmas.
Berdasarkan data rekam medik, diketahui populasi pasien DM di Puskesmas tersebut adalah 255 orang.
Dengan menggunakan rumus diatas, maka diketahui:
N : 255 (besar populasi)
Z(1-a/2) : 1,96 (tingkat kepercayaan yang dipilih adalah 95%)
P : 0,5 (karena kita tidak tahu proporsi kejadiannya)
d : 0,1 (karena besar penyimpangan terhadap populasi yang diinginkan adalah 10%)
Setelah dimasukan sesuai rumus, maka:
n = ((255) (1,96)2 0,5 (1 – 0,5)) / (255) ((0,1)2 + (1,96)2 0,5 (1 – 0,5))
n = (244,9) / (3,5104)
n = 69,7
n = 70 (dibulatkan)
Rumus sampel bila jumlah populasi tidak diketahui
Berikut adalah rumus sampel bila jumlah populasinya tidak kita ketahui (Adiputra, 2021):

Keterangan:
n : besar sampel
Z(1-a/2) : nilai sebaran normal baku, besarnya tergantung tingkat kepercayaan (TK), jika TK 90%, maka nilai 1,64, TK 95% = 1,96, TK 99% = 2,57.
Z (1 – β) : nilai sebaran normal baku, (kekuatan uji/power of test 90% = 1,282 dan power of test 80% = 0,842)
P : Proporsi kejadian, Q = 1 – P
P1 : Proporsi kejadian 1, Q1 = 1 – P1
P2 : Proporsi kejadian 2, Q2 = 1 – P2
Contoh penghitungan jumlah sampel dengan rumus sampel populasi tidak diketahui
Kita ingin meneliti untuk melihat perbedaan proporsi kesembuhan luka pasien DM yang diobati dengan teknik perawatan luka menggunakan modern dressing dengan teknik perawatan luka menggunakan moist wound healing.
Berdasarkan data rekam medis, diketahui bahwa proporsi pasien sembuh dengan modern dressing adalah 75%. Menurut pertimbangan klinis perbedaan keduanya adalah 10%.
Dengan menggunakan rumus diatas, diketahui:
Z(1-a/2) : 1,96 (tingkat kepercayaan yang dipilih adalah 95%)
Z (1 – β) : 0,842 (kita pilih kekuatan uji/power of test 80%)
P1 : Q1 = 1 – 0,75 = 0,25 (nilai 0,75 didapatkan karena proporsi kesembuhan dengan modern dressing adalah 75%)
P2 : Q2 = 1 – 0,85 = 0,15 (nilai 0,5 didapatkan karena perbedaan keduanya adalah 10% menurut pertimbangan klinis)
P = (P1 + P2) / 2 = (0,75 + 0,85) / 2 = 0,8 proporsi kejadian, maka Q = 1 – 0,8 = 0,2
Setelah dimasukan sesuai rumus, maka:
n = (1,96 x √(0,8 x 0,2) + 0,842 x √(0,75 x 0,25) + √(0,85 x 0,15)2 / (0,75 – 0,85)2
n = (2,5) / (0,01)
n = 250
Jadi besaran sampel minimal yang diperlukan adalah 250 orang.
Kesimpulan
Menentukan populasi, teknik sampling, dan rumus sampel penelitian keperawatan dilakukan secara bersamaan.
Silahkan penghitungan sampel sesuai contoh diatas sesuai penelitian anda.
Setelah mendapatkan jumlah sampel ideal, berikutnya pilih teknik sampling sesuai dengan kebutuhan penelitian anda.
Bila ada yang ingin ditanyakan silahkan ketik pada kolom komentar. Kami akan mencoba yang terbaik untuk menjawab pertanyaan anda.
Referensi asli penghitungan rumus sampel bisa anda lihat dalam buku Adiputra (2021) yang berjudul Metodologi Penelitian Kesehatan, terbitan Yayasan Kita Menulis.
Sukses dan salam sehat.
Referensi
- Adiputra, I. M. S. (2021). Metodologi Penelitian Kesehatan. Yayasan Kita Menulis.
- Darsini, Fahrurrozi, & Cahyono, E. A. (2019). Pengetahuan: Artikel Review. Jurnal Keperawatan, 12(1), 95–107.
- Indarwati., Maryatun., Purwaningsih, W., Andriani, A., & Siswanto. (2020). Penerapan Metode Penelitian dalam Praktik Keperawatan Komunitas Lengkap dengan Contoh Proposal. Solo: CV. Indotama Solo.
- Masturoh, I., & Anggita T, N. (2018). Metodologi Penelitian Kesehatan. Kementrian Kesehatan Republik Indonesia Pusat Pendidikan Sumber Daya Manusia Kesehatan.
- File pribadi.
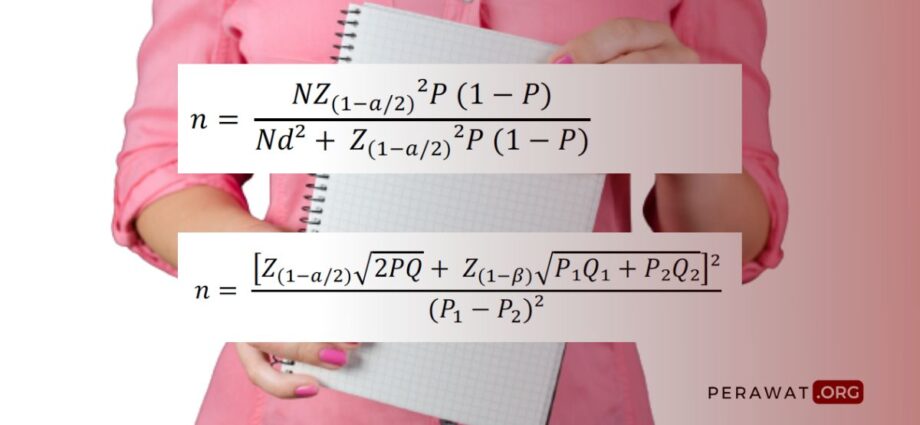
Mengapa menentukan populasi merupakan langkah awal yang penting sebelum mempelajari Teknik Sampling dan Rumus Sampel dalam penelitian? Salam Telkom University